(本小题满分10分)选修4-4坐标系与参数方程
在平面直角坐标系中,取原点为极点,x轴正半轴为极轴建立极坐标系,已知曲线C1的极坐标方程为 ,直线C2的参数方程为:
,直线C2的参数方程为: (t为参数)
(t为参数)
(I )求曲线C1的直角坐标方程,曲线C2的普通方程.
(II)先将曲线C1上所有的点向左平移1个单位长度,再把图象上所有点的横坐标伸长到原来的 倍得到曲线C3 P为曲线C3上一动点,求点P到直线C2距离的最小值,并求出相应的P点的坐标.
倍得到曲线C3 P为曲线C3上一动点,求点P到直线C2距离的最小值,并求出相应的P点的坐标.
(本小题满分12分)如图,已知平面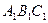 平行于三棱锥
平行于三棱锥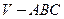 的底面,等边三角形
的底面,等边三角形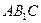 所在平面与面
所在平面与面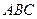 垂直,且
垂直,且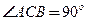 ,设
,设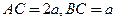 。
。
(Ⅰ)证明: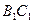 为异面直线
为异面直线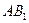 与
与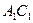 的公垂线;
的公垂线;
(Ⅱ)求点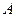 与平面
与平面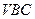 的距离;
的距离;
(Ⅲ)求二面角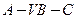 的大小。
的大小。
(本小题满分12分)已知函数 满足
满足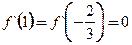 ,
,
(Ⅰ)求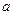 、
、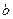 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若对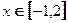 ,不等式
,不等式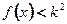 恒成立,求
恒成立,求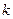 的取值范围。
的取值范围。
(本小题满分12分)贵阳六中织高二年级4个班的学生到益佰制药厂、贵阳钢厂、贵阳轮胎厂进行社会实践,规定每个班只能在这3个厂中任选择一个,假设每个班选择每个厂的概率是等可能的。(Ⅰ)求3个厂都有班级选择的概率;(Ⅱ)用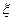 表示有班级选择的厂的个数,求随机变量
表示有班级选择的厂的个数,求随机变量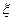 的概率分布及数学期望
的概率分布及数学期望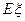 。
。
(本小题满分12分)已知向量 且
且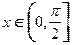 ,(Ⅰ)若
,(Ⅰ)若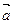 与
与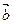 是两个共线向量,求
是两个共线向量,求 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的最小值及相应的
的最小值及相应的 的值。
的值。
(理)(本小题共14分)已知函数
(1)若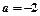 时,函数
时,函数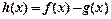 在其定义域内是增函数,求b的取值范围
在其定义域内是增函数,求b的取值范围
(2)在(1)的结论下,设函数 ,求函数
,求函数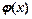 的最小值;(3)设函数
的最小值;(3)设函数 的图象C1与函数
的图象C1与函数 的图象C2交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。
的图象C2交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。