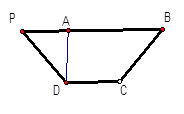
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=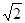 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
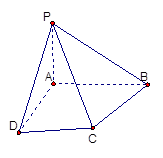
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分 .
.
(本小题12分)已知函数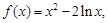

(Ⅰ)求函数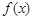 的极值;
的极值;
(Ⅱ)设函数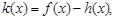 若函数
若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值范围.
的取值范围.
(本小题12分)设 .
.
(1)求函数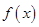 的单调区间;
的单调区间;
(2)若当 时
时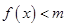 恒成立,求
恒成立,求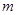 的取值范围
的取值范围
(本小题满分12分).设命题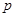 :“方程
:“方程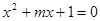 有两个实数根”;命题
有两个实数根”;命题 :“方程
:“方程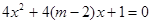 无实根”,若
无实根”,若 为假,
为假,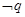 为假,求实数
为假,求实数 的取值范围.
的取值范围.
(本题15分)已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆
(1)求实数m的取值范围;
(2)求该圆半径r的取值范围;
(3)求圆心的轨迹方程。
(本题15分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.