（本小题满分12分）已知椭圆
经过点
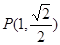，且两焦点与短轴的一个端点的连线构成等腰直角三角形．
（1）求椭圆的方程；
（2）动直线
交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得以AB为直径的圆恒过点T。若存在，求出点T的坐标；若不存在，请说明理由．
已知函数y=f(x)的定义域为R，且对任意a,b∈R,都有f(a+b)=f(a)+f(b)，且当x＞0时，f(x)＜0恒成立，f(3)="-3."
(1)证明：函数y=f(x)是R上的减函数；
（2）证明：函数y=f(x)是奇函数；
（3）试求函数y=f(x)在［m,n］（m,n∈Z）上的值域.
判断下列各函数的奇偶性：
（1）f（x）=（x-2）
；
（2）f（x）=
；
（3）f（x）=
已知函数f(x)的定义域为R，且满足f(x+2)=-f(x).
（1）求证：f(x)是周期函数；
（2）若f(x)为奇函数，且当0≤x≤1时，f(x)=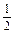
x,求使f(x)=-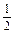在［0，2 009］上的所有x的个数.
求下列函数的最值与值域：
（1）y=4-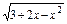
;(2)y=2x-
;
(3)y=x+
;(4)y=
.
某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时，可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元，未租出的车每辆每月需要维护费50元.
（1）当每辆车的月租金定为3 600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？