已知函数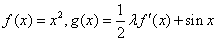 ,其中函数
,其中函数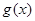 在
在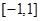 上是减函数.
上是减函数.
(1)求曲线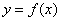 在点
在点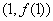 处的切线方程;
处的切线方程;
(2)若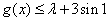 在
在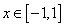 上恒成立,求
上恒成立,求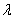 得取值范围.
得取值范围.
(3)关于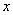 的方程
的方程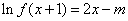 ,
,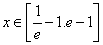 有两个实根,求
有两个实根,求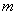 的取值范围.
的取值范围.
如图分别是正三棱台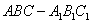 的直观图和正视图,
的直观图和正视图,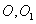 分别是上下底面的中心,
分别是上下底面的中心,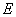 是
是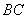 中点.
中点.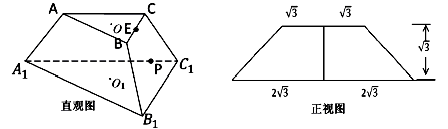
(1)求正三棱台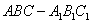 的体积;(注:棱台体积公式:
的体积;(注:棱台体积公式: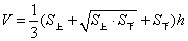 ,其中
,其中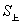 为棱台上底面面积,
为棱台上底面面积,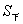 为棱台下底面面积,
为棱台下底面面积,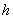 为棱台高);
为棱台高);
(2)求平面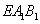 与平面
与平面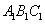 的夹角的余弦;
的夹角的余弦;
(3)若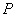 是棱
是棱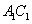 上一点,求
上一点,求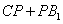 的最小值.
的最小值.
 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰 的长为3(百米),底
的长为3(百米),底 的长为4(百米).现决定在空地内筑一条笔直的小路
的长为4(百米).现决定在空地内筑一条笔直的小路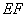 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为 和
和 .
.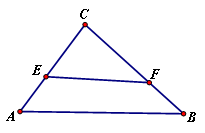
(1)若小路一端 为
为 的中点,求此时小路的长度;
的中点,求此时小路的长度;
(2)若小路的端点 两点分别在两腰上,求
两点分别在两腰上,求 得最小值.
得最小值.
已知数列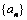 满足
满足 .
.
(Ⅰ)证明数列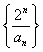 是等差数列;
是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设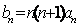 ,求数列
,求数列 的前
的前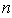 项和
项和 .
.
已知函数
(1)求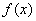 得最小正周期;
得最小正周期;
(2)求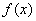 在区间
在区间 上的取值范围.
上的取值范围.