甲乙两个学校高三年级分别有1100人和1000人,为了了解这两个学校全体高三年级学生在该地区二模考试中的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统汁表,规定考试成绩在[120,150]内为优秀.
(I)试求x,y的值;
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。
(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附:
设函数 .
.
(1)解不等式 ;
;
(2)已知关于x的不等式 恒成立,求实数
恒成立,求实数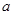 的取值范围.
的取值范围.
已知函数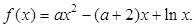
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当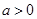 时,若
时,若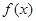 在区间
在区间 上的最小值为
上的最小值为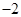 ,其中
,其中 是自然对数的底数,
是自然对数的底数,
求实数 的取值范围;
的取值范围;
巴西世界杯足球赛正在如火如荼进行.某人为了了解我校学生“通过电视收看世界杯”是否与性别有关,从全校学生中随机抽取30名学生进行了问卷调查,得到了如下列联表:
| 男生 |
女生 |
合计 |
|
| 收看 |
10 |
||
| 不收看 |
8 |
||
| 合计 |
30 |
已知在这30名同学中随机抽取1人,抽到“通过电视收看世界杯”的学生的概率是 .
.
(I)请将上面的列联表补充完整,并据此资料分析“通过电视收看世界杯”与性别是否有关?
(II)若从这30名同学中的男同学中随机抽取2人参加一活动,记“通过电视收看世界杯”的人数为X,求X的分布列和均值.
  |
0.100 |
0.050 |
0.010 |
 |
2.706 |
3.841 |
6.635 |
(参考公式: ,
,  )
)
某校举行综合知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有6次答题的机会,选手累计答对4题或答错3题即终止其初赛的比赛,答对4题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响).
(Ⅰ)求选手甲回答一个问题的正确率;
(Ⅱ)求选手甲可以进入决赛的概率.
设函数
(Ⅰ)若 ,解不等式
,解不等式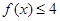 ;
;
(Ⅱ)若函数 有最小值,求
有最小值,求 的取值范围.
的取值范围.