某校为了更好地落实新课改,增加研究性学习的有效性,用分层抽样的方法从其中A、B、C三个学习小组中,抽取若干人进行调研,有关数据见下表(单位:人)
(1)求表中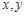 的值
的值
| 学习小组 |
小组人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
(2)若从B、C学习小组抽取的人中选2人作感想发言,求这2人都来自C学习小组的概率.
已知等差数列{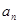 },公差
},公差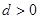 ,
,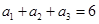 ,且
,且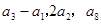 成等比数列.
成等比数列.
(I)求{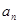 }的通项公式;
}的通项公式;
(II)设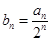 ,求证:
,求证: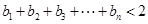 .
.
在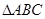 中,内角
中,内角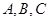 对边分别为
对边分别为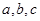 ,且
,且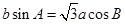 .
.
(Ⅰ)求角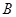 的大小;
的大小;
(Ⅱ)若 ,求
,求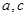 的值.
的值.
(本小题满分14分)
已知函数 (
( ).
).
(1)若 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 的最小值是1,求实数
的最小值是1,求实数 的值.
的值.
(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
(本小题满分14分)
已知函数 (
( ),且
),且 .
.
(1)求α的值;
(2)求函数 的零点;
的零点;
(3)判断 在(-∞,0)上的单调性,并给予证明.
在(-∞,0)上的单调性,并给予证明.