(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
设向量 ,过定点
,过定点 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点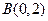 ,以向量
,以向量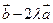 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
(1)求点P的轨迹C的方程;
(2)设过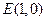 的直线
的直线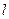 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求 的取值范围
的取值范围
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标。
在平面直角坐标系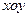 中,设点
中,设点 (1,0),直线
(1,0),直线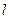 :
: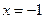 ,点
,点 在直线
在直线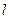 上移动,
上移动, 是线段
是线段 与
与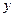 轴的交点,
轴的交点, 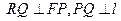 .
.
(Ⅰ)求动点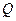 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记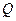 的轨迹的方程为
的轨迹的方程为 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线 的弦
的弦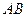 、
、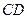 ,设
,设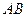 、
、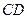 的中点分别为
的中点分别为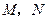 .求证:直线
.求证:直线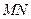 必过定点
必过定点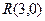 .
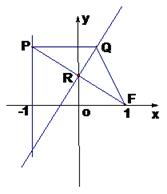
.
已知椭圆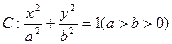 的离心率为
的离心率为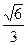 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且 ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当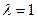 时.,
时.,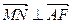 ;
;
(2)若当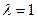 时有
时有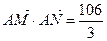 ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当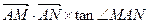 的值为6
的值为6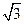 时, 求出直线MN的方程.
时, 求出直线MN的方程.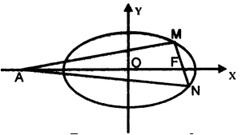
设直线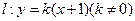 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: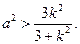 ;
;
(2)若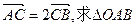 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.