三棱柱 中,
中,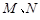 分别是
分别是 、
、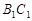 上的点,且
上的点,且 ,
, 。设
。设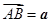 ,
, ,
, .
.
(Ⅰ)试用 表示向量
表示向量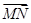 ;
;
(Ⅱ)若 ,
, ,
, ,求MN的长.。
,求MN的长.。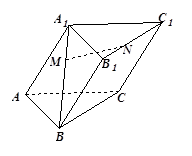
已知椭圆C的中心在原点,焦点在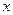 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的 倍且经过点M
倍且经过点M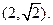
(Ⅰ)求椭圆C的方程
(Ⅱ)过圆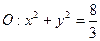 上的任一点作圆的一条切线交
上的任一点作圆的一条切线交 椭圆C与A、B两点
椭圆C与A、B两点
①求证: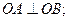
②求|AB|的取值范围
.已知函数 ,
, 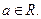
(1)若函数 在
在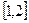 上是减函数,求实数
上是减函数,求实数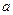 的取值范围
的取值范围
(2)令 ,是否存在实数
,是否存在实数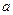 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出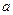 的值;若不存在,说明理由
的值;若不存在,说明理由
(3)当
 时,证明:
时,证明: 
如图,在直三棱柱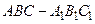 中,
中,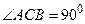 ,
,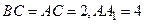 ,
,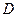 为棱
为棱 上的一点,
上的一点, 分别为
分别为 、
、 的重心.
的重心.
(1)求证: ;
;
(2)若二面角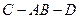 的正切值为
的正切值为 ,求两个半平面
,求两个半平面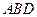 、
、 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(可选)若点 在平面
在平面 的射影正好为
的射影正好为 ,试判断
,试判断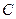 在平面
在平面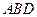 的射影是否为
的射影是否为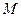 .
.
小学三年级的英语老师要求学生从星期一到星期四每天学习英语单词3个;每周星期五对一周内所学单词随机抽取4个进行检测(一星期所学的单词每个被抽到的可能性相同);
(1)求英语老师随机抽到的4个单词中,至少含有3个离周五最近两天学习过的概率;
(2)某学生在周五检测中,对其最近两天所学过的单词每个能默写对的概率为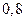 ,对周一和周二的单词每个能默写对的概率为
,对周一和周二的单词每个能默写对的概率为 ;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数
;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数 的分布列和期望.
的分布列和期望.
已知向量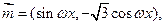
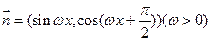 ,若函数
,若函数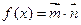 的最小正周期为
的最小正周期为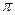
(Ⅰ)求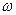 的值
的值
(Ⅱ)若将函数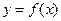 的图象向右平移
的图象向右平移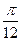 个单位,再将所得到的图象上各点的横坐标伸长到原来的
个单位,再将所得到的图象上各点的横坐标伸长到原来的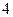 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象,求
的图象,求 的单调递减区间
的单调递减区间