命题p:关于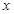 的不等式
的不等式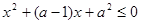 的解集为
的解集为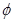 ;
;
命题q:函数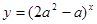 为增函数.
为增函数.
分别求出符合下列条件的实数 的取值范围.
的取值范围.
(1)p、q至少有一个是真命题;(2)p∨q是真命题且p∧q是假命题.
已知函数f(x)=x2+2x+alnx(a∈R).
(1)当时a=﹣4时,求f(x)的最小值;
(2)若函数f(x)在区间(0,1)上为单调函数,求实数a的取值范围.
已知各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N*,有 2Sn=2 .函数f(x)=x2+x,数列{bn}的首项b1=
.函数f(x)=x2+x,数列{bn}的首项b1= .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令 求证:{cn}是等比数列并求{cn}通项公式;
求证:{cn}是等比数列并求{cn}通项公式;
(Ⅲ)令dn=an•cn,(n为正整数),求数列{dn}的前n项和Tn.
已知数列{an}的前n项和Sn,a1=﹣ ,Sn+
,Sn+ (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn= ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣ .
.
(Ⅰ)求右焦点坐标是(2,0),且经过点 的椭圆的标准方程
的椭圆的标准方程
(Ⅱ)求与椭圆 共焦点且过点
共焦点且过点 的双曲线的标准方程.
的双曲线的标准方程.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线 没有交点,求b的取值范围.
没有交点,求b的取值范围.
(3)设 ,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.