某小区每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图
设命题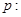
 和
和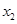 是方程
是方程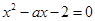 的两个根,不等式
的两个根,不等式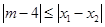 对任意实数
对任意实数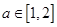 恒成立;命题Q:函数
恒成立;命题Q:函数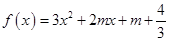 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数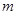 的取值范围.
的取值范围.
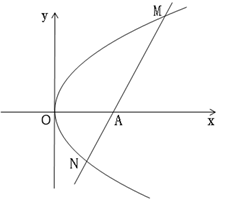
已知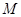 为抛物线
为抛物线 上一动点,
上一动点,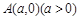 为其对称轴上一点,直线
为其对称轴上一点,直线 与抛物线的另一个交点为
与抛物线的另一个交点为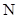 .当
.当 为抛物线的焦点且直线
为抛物线的焦点且直线 与其对称轴垂直时,△
与其对称轴垂直时,△ 的面积为
的面积为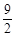 .
.
(1)求抛物线的标准方程;
(2)记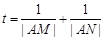 ,若
,若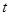 的值与
的值与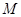 点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
定点”,若没有,请说明理由.
已知动点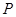 与两定点
与两定点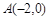 、
、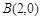 连线的斜率之积为
连线的斜率之积为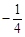 .
.
(1)求动点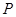 的轨迹C的方程;
的轨迹C的方程;
(2)若过点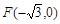 的直线
的直线 交轨迹
交轨迹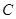 于M、N两点,且轨迹
于M、N两点,且轨迹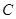 上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线
上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线 的方程.
的方程.
直三棱柱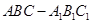 中,
中,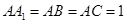 ,
,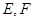 分别是
分别是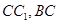 的中点,
的中点,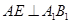 ,
,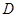 为棱
为棱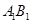 上的点.
上的点.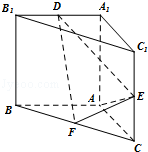
(1)证明: ;
;
(2)是否存在一点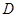 ,使得平面
,使得平面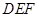 与平面
与平面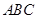 所成锐二面角的余弦值为
所成锐二面角的余弦值为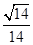 ?
?
若存在,说明点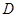 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
已知双曲线 的方程为:
的方程为:
(1)求双曲线 的离心率;
的离心率;
(2)求与双曲线 有公共的渐近线,且经过点
有公共的渐近线,且经过点 (
( )的双曲线的方程.
)的双曲线的方程.