在海岸A处，发现北偏东
方向，距离A为
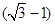海里的B处有一走私船，在A北偏西
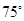方向距离A为2海里的C处有我方一艘缉私艇奉命以
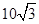海里/小时的速度追截走私 船，且C在B的正西方，此时走私船正以
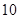海里/小时的速度从B处向北偏东
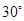方向逃窜， 问缉私艇沿什么方向，才能最快追上走私船？需要多长时间？
某体育杂志针对2014年巴西世界杯发起了一项调查活动，调查“各球队在世界杯的名次与该队历史上的的实力和表现有没有关系”，在所有参与调查的人中，持“有关系”“无关系”“不知道”态度的人数如表所示：
| 有关系 |
无关系 |
不知道 |
|
| 40岁以下 |
800 |
450 |
200 |
| 40岁以上（含40岁） |
100 |
150 |
300 |
（1）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从持“有关系”态度的人中抽取45人，求n的值，并求从持其他两种态度的人中应抽取的人数；
（2）在持“不知道”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任选取2人，求至少一人在40岁以下的概率.
已知函数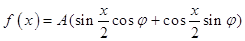
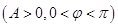的最大值是2，且
．
（1）求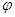
的值；
（2）已知锐角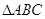
的三个内角分别为
，
，
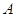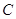，若
，求
的值．
已知函数f（x）=x•lnx（e为无理数，e≈2.718）
（1）求函数f（x）在点（e，f（e））处的切线方程；
（2）设实数a＞
，求函数f（x）在[a，2a]上的最小值；
（3）若k为正数，且f（x）＞（k﹣1）x﹣k对任意x＞1恒成立，求k的最大值．
已知椭圆C：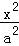
+
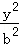=1（a＞b＞0）的离心率是
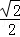，且点P（1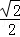，）在椭圆上．
（1）求椭圆的方程；
（2）若过点D（0，2）的直线l与椭圆C交于不同的两点E，F，试求△OEF面积的取值范围（O为坐标原点）．
已知四边形ABCD是矩形，AB=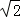
，BC=
，将△ABC沿着对角线AC折起来得到△AB1C，且顶点B1在平面AB=CD上射影O恰落在边AD上，如图所示．
（1）求证：AB1⊥平面B1CD；
（2）求三棱锥B1﹣ABC的体积VB1﹣ABC．