(本小题满分15分)已知函数 .
.
(1)若函数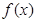 的值域为
的值域为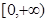 ,求a的值;
,求a的值;
(2)若函数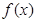 在
在 上是增函数,求实数
上是增函数,求实数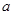 的取值范围.
的取值范围.
(本小题满分15分)定义在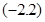 上的奇函数
上的奇函数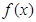 ,满足
,满足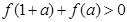 ,又当
,又当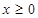 时,
时,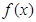 是减函数,求
是减函数,求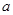 的取值范围。
的取值范围。
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?
(本小题满分13分)已知函数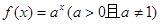 经过点
经过点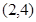 .
.
(1)求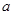 的值;(2)求
的值;(2)求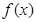 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.
(本小题满分14分)如图椭圆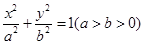 的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。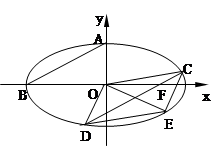
(Ⅰ)求椭圆的离心率;
(Ⅱ)若平行四边形OCED的面积为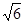 , 求椭圆的方程.
, 求椭圆的方程.