已知椭圆C: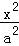 +
+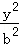 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是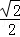 ,且点P(1,
,且点P(1,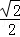 )在椭圆上.
)在椭圆上.
(1)求椭圆的方程;
(2)若过点D(0,2)的直线l与椭圆C交于不同的两点E,F,试求△OEF面积的取值范围(O为坐标原点).
(本题满分14分)已知集合
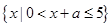 ,集合
,集合

(Ⅰ)若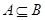 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)若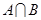 是单元素集合求实数
是单元素集合求实数 的值.
的值.
(本小题满分14分)
设函数 .
.
(Ⅰ)当 时,求函数
时,求函数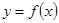 的单调区间;
的单调区间;
(Ⅱ)已知 ,若函数
,若函数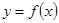 的图象总在直线
的图象总在直线 的下方,求
的下方,求 的取值范围;
的取值范围;
(Ⅲ)记 为函数
为函数 的导函数.若
的导函数.若 ,
,
试问:在区间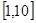 上是否存在
上是否存在 (
(
 )个正数
)个正数 …
… ,使得
,使得 成立?请证明你的结论.
成立?请证明你的结论.
(本小题满分12分)
函数 .
.
(Ⅰ)若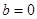 ,且
,且 在
在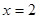 处取得极小值,求实数
处取得极小值,求实数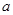 的值;
的值;
(Ⅱ)若函数 在
在 上是增函数,试探究
上是增函数,试探究 应满足什么条件;
应满足什么条件;
(Ⅲ)若 ,不等式
,不等式 对任意
对任意 恒成立,求整数
恒成立,求整数 的最大值.
的最大值.
(本小题满分12分)
某分公司经销某种产品,每件产品的成本为3元,并且每件产品需向总公司交纳6元的管理费,预计当每件产品的售价为x元(9 ≤ x ≤ 11)时,一年的销售量为 万件。(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
万件。(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润L最大?
(本小题满分12分)
已知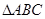 是复平面内的三角形,
是复平面内的三角形, 两点对应的复数分别为
两点对应的复数分别为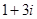 和
和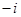 ,且
,且 ,
,
(Ⅰ)求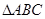 的顶点C的轨迹方程。
的顶点C的轨迹方程。
(Ⅱ)若复数 满足
满足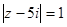 ,探究复数
,探究复数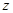 对应的点
对应的点 的轨迹与顶点C的轨迹的位置关系。
的轨迹与顶点C的轨迹的位置关系。