已知圆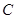 的参数方程为
的参数方程为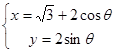 (
( 为参数),
为参数),
(1)以原点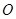 为极点、
为极点、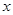 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆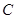 的极坐标方程;
的极坐标方程;
(2)已知直线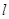 经过原点
经过原点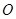 ,倾斜角
,倾斜角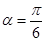 ,设
,设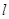 与圆
与圆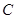 相交于
相交于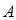 、
、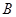 两点,求
两点,求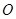 到
到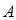 、
、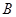 两点的距离之积。
两点的距离之积。
如图,SA⊥平面ABCD,四边形ABCD为正方形,SA= ,AB=1.
,AB=1.
(1)求证:AB⊥平面SAD
(2)求异面直线AB与SC所成角的大小.
已知等比数列 中,
中, .求
.求
(1)等比数列 的通项公式;
的通项公式;
(2)数列 的前6项和
的前6项和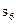
已知三角形ABC的三个内角∠A、∠B、∠C所对的边长分别为a、b、c,且A是锐角,sinA=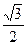 ,c="2" ,b=3.
,c="2" ,b=3.
(1)求cosA , tanA
(2)求a的值.
(本小题满分14分)
设数列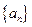 的前
的前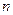 项和为
项和为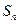 ,已知
,已知 ,
,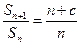 (
(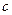 为常数,
为常数,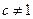 ,
,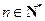 ),且
),且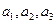 成等差数列.
成等差数列.
(1)求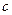 的值;
的值;
(2)求数列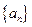 的通项公式;
的通项公式;
(3)若数列 是首项为1,公比为
是首项为1,公比为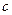 的等比数列,记
的等比数列,记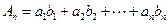 ,
,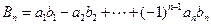 ,
,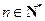 .证明:
.证明: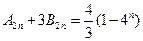 .
.
(本小题满分14分)
已知 的周长为
的周长为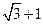 ,且
,且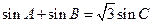 ,
, 的面积为
的面积为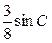 ,
,
(1)求边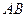 的长;
的长;
(2)求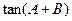 的值.
的值.