在平面直角坐标系xOy中,已知ΔPAB的顶点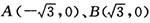 ,P为动点,且
,P为动点,且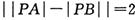 .记动点P的轨迹为曲E
.记动点P的轨迹为曲E
(I) 求曲线E的方程;
(II)设l是既不与AB平行也不与AB垂直的直线,且原点O到直线l的距离为 ,l与曲线E相交于不同的两点G、H,问
,l与曲线E相交于不同的两点G、H,问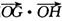 的值是否为定值?若为定值,求出此定值;若不是,请说明理由.
的值是否为定值?若为定值,求出此定值;若不是,请说明理由.
设直线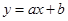 与双曲线
与双曲线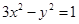 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点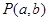 的轨迹方程.
的轨迹方程.
已知椭圆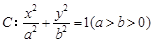 的离心率为
的离心率为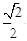 ,其中左焦点
,其中左焦点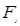 (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
设命题 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :实数
:实数 满足
满足 且
且 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
已知椭圆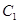 的方程为
的方程为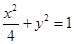 ,双曲线
,双曲线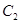 的左、右焦点分别为
的左、右焦点分别为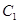 的左、右顶点,而
的左、右顶点,而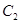 的左、右顶点分别是
的左、右顶点分别是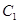 的左、右焦点,
的左、右焦点,
(1)求双曲线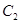 的方程;
的方程;
(2)若直线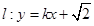 与椭圆
与椭圆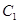 及双曲线
及双曲线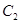 都恒有两个不同的交点,且
都恒有两个不同的交点,且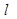 与
与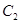 的两个交点A和B满足
的两个交点A和B满足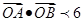 (其中0为原点),求k的取值范围。
(其中0为原点),求k的取值范围。
已知双曲线方程2x2-y2=2.
(1)求以A(2,1)为中点的双曲线的弦所在的直线方程;
(2)过点(1,1)能否作直线l,使l与双曲线交于Q1,Q2两点,且Q1,Q2两点的中点为(1,1)?如果存在,求出它的方程;如果不存在,说明理由.