椭圆方程为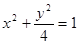 ,过点
,过点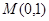 的直线
的直线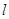 交椭圆于
交椭圆于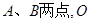 为坐标原点,点
为坐标原点,点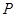 满足
满足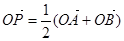 ,当
,当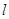 绕点
绕点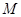 旋转时,求动点
旋转时,求动点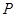 的轨迹方程.
的轨迹方程.
(1)化简 ;
;
(2)化简
已知△ABC的两个顶点A(-10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.
已知函数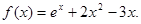
(I)求曲线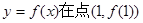 处的切线方程;
处的切线方程;
(II)当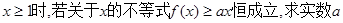 的取值范围.
的取值范围.
如图,已知椭圆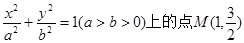 到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点..
到它的两焦点F1、F2的距离之和为4,A、B分别是它的左顶点和上顶点..
(I)求此椭圆的方程及离心率;
(II)平行于AB的直线l与椭圆相交于P、Q两点,求|PQ|的最大值及此时直线l的方程.
甲乙两车间生产同一种产品,各生产40个后,按产品合格与不合格进行统计,甲车间生产的产品合格数为36个,乙车间生产的产品合格数为24个.
(1)根据以上数据完成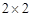 列联表;
列联表;
| 不合格 |
合格 |
总计 |
|
| 甲车间 |
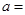 |
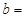 |
|
| 乙车间 |
 |
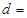 |
|
| 总计 |
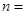 |
(2)试判断是否产品合格与生产车间是否有关?