泉州火车站有甲种货物60吨,乙种货物90吨,现计划用30节A、B两种型号的车厢将这批货物运出.设30节车厢中有A型车厢 节,
节,请用含
 的代数式表示30节车厢中有B型车厢的节数;
的代数式表示30节车厢中有B型车厢的节数;如果甲种货物全部用A型车厢运送,乙种货物全部用B型车厢运送,则A型、B型车厢平均每节运送的货物吨数刚好相同,请求出
 的值;
的值;在(2)的条件下,已知每节A型车厢的运费是
 万元,每节B型车厢的运费比每节A型车厢的运费少1万元,设总运费为
万元,每节B型车厢的运费比每节A型车厢的运费少1万元,设总运费为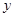 万元,求
万元,求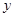 与
与 之间的函数关系式.如果已知每节A型车厢的运费不超过5万元,而每节B型车厢的运费又不低于3万元,求总运费
之间的函数关系式.如果已知每节A型车厢的运费不超过5万元,而每节B型车厢的运费又不低于3万元,求总运费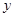 的取值范围.
的取值范围.
如图,在△ABC中,D、E分别是AB、AC的中点.BE=2DE,延长DE到点F,使得EF=BE,连接CF. 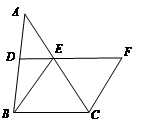
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
李大爷几年前承包了甲、乙两片荒山,各栽100棵杨梅树,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量数如折线统计图所示.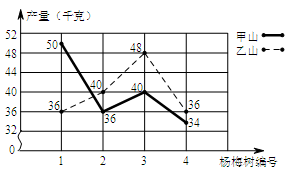
(1)分别计算甲、乙两片山上杨梅产量数样本的平均数;
(2)试通过计算说明,哪片山上的杨梅产量较稳定?
如图,从热气球P上测得两建筑物A、B的底部的俯角分别为45°和30°,如果A、B两建筑物的距离为60米,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果保留根号)
解方程:(1)x2+10="7x" (2)2x2+4x-5=0
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.