如图,斜三棱柱 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是 的中点,且
的中点,且 .
.
(1)求证:平面
 平面
平面 ;
;
(2)若二面角 的余弦值为
的余弦值为 ,设
,设 ,求
,求 的值.
的值.
(本小题满分10分)选修4-1:几何证明选讲
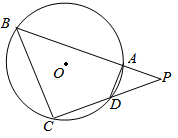
如图,四边形ABCD是圆 的内接四边形,延长BA和CD相交于点P,
的内接四边形,延长BA和CD相交于点P, ,
, .
.
(Ⅰ)求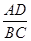 的值;
的值;
(Ⅱ)若BD为圆 的直径,且
的直径,且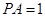 ,求BC的长.
,求BC的长.
(本小题满分12分)已知函数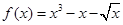 .
.
(Ⅰ)求函数 的零点的个数;
的零点的个数;
(Ⅱ)令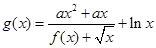 ,若函数
,若函数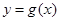 在
在 内有极值,求实数a的取值范围.
内有极值,求实数a的取值范围.
(本小题满分12分)已知椭圆
 ,
, 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
(1)求椭圆C的方程;
(2)设直线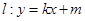 ,
, 与椭圆C相交于A、B两点,以线段OA,OB为邻边作平行四边形OAPB,其中顶点P在椭圆C上,O为坐标原点,求
与椭圆C相交于A、B两点,以线段OA,OB为邻边作平行四边形OAPB,其中顶点P在椭圆C上,O为坐标原点,求 的取值范围.
的取值范围.
(本小题满分12分)在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD 平面ABCD,
平面ABCD,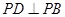 ,
, .
.
(Ⅰ)求证:平面PCD 平面PAB;
平面PAB;
(Ⅱ)设E是棱AB的中点, ,
,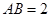 ,求二面角
,求二面角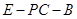 的余弦值.
的余弦值.
(本小题满分12分)由于雾霾日趋严重,政府号召市民乘公交出行,但公交车的数量太多会造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的60名候车乘客中进行随机抽样,共抽取10人进行调查反馈,所选乘客情况如下表所示: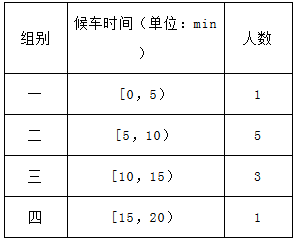
(Ⅰ)估计这60名乘客中候车时间少于10分钟的人数;
(Ⅱ)现从这10人中随机取3人,求至少有一人来自第二组的概率;
(Ⅲ)现从这10人中随机抽取3人进行问卷调查,设这3个人共来自X个组,求X的分布列及数学期望.