已知A、D分别为椭圆E: 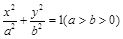 的左顶点与上顶点,椭圆的离心率
的左顶点与上顶点,椭圆的离心率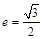 ,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且
,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且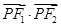 的最大值为1 .
的最大值为1 .
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA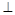 OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
(3)设直线l与圆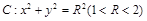 相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
(本小题满分13分)
如图,在直三棱柱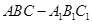 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中, 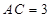 ,
,  ,
,  ,
, 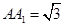 ,点
,点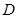 是
是 的中点.
的中点. 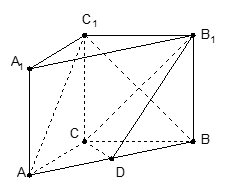
(Ⅰ) 求证: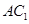 ∥平面
∥平面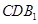 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
(本小题满分13分)
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.
(Ⅰ)求证:AD⊥平面SBC;
(Ⅱ)试在SB上找一点E,使得平面ABS⊥平面ADE,并证明你的结论.
(本小题满分13分)
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(Ⅲ)在这次测试中,学生跳绳次数的中位数、众数各是是多少?(精确到0.1)
已知函数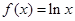 ,
,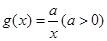 ,设
,设 .
.
(1)求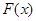 的单调区间;
的单调区间;
(2)若以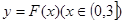 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率
恒成立,求实数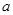 的最小值.
的最小值.
(3)是否存在实数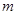 ,使得函数
,使得函数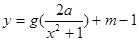 的图象与
的图象与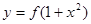 的图
的图
象恰好有四个不同的交点?若存在,求出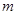 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
已知椭圆 .过点
.过点 作圆
作圆 的切线
的切线 交椭圆
交椭圆 于
于 ,
, 两点.
两点.
(1)求椭圆 的焦点坐标和离心率;
的焦点坐标和离心率;
(2)将 表示为
表示为 的函数,并求
的函数,并求 的最大值.
的最大值.