一边长为 的正方形铁片,铁片的四角各截去一个边长为
的正方形铁片,铁片的四角各截去一个边长为 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(Ⅰ)试把方盒的体积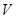 表示为
表示为 的函数;
的函数;
(Ⅱ) 多大时,方盒的体积
多大时,方盒的体积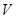 最大?
最大?
(本小题满分l2分)
已知△ABC的三个内角A,B,C所对的边分别为



 且
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若
 求
求 △ABC。
△ABC。
(本小题满分14分

 )
)
设数列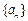 为等比数列,数列
为等比数列,数列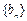 满足
满足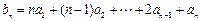 ,
,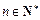 ,已知
,已知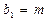 ,
,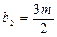 ,其中
,其中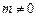 .
.
(Ⅰ) 求数列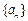 的首项和公比;
的首项和公比;
(Ⅱ)当m=1时,求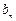 ;
;
(Ⅲ)设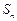 为数列
为数列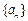 的前
的前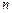 项和,若对于任意的正整数
项和,若对于任意的正整数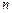 ,都有
,都有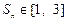 ,求实数
,求实数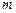 的取值范围.
的取值范围.
(本小题满分14分)
已知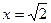 是函数
是函数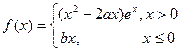 的极值点.
的极值点.
(Ⅰ) 当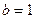 时,求函数
时,求函数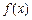 的单调区间;
的单调区间;
(Ⅱ)当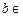 R时,函数
R时,函数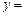
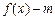 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(本小题满分14分)
给定椭圆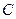 :
: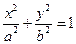
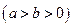 ,称圆心在坐标原点
,称圆心在坐标原点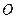 ,半径为
,半径为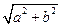 的圆是椭圆
的圆是椭圆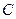 的“伴随圆”. 已知椭圆
的“伴随圆”. 已知椭圆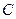 的两个焦点分别是
的两个焦点分别是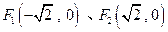 ,椭圆
,椭圆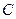 上一动点
上一动点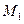 满足
满足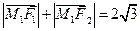 .
.
(Ⅰ) 求椭圆
求椭圆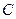 及其“伴随圆”的方程;
及其“伴随圆”的方程; (Ⅱ) 过点P
(Ⅱ) 过点P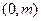
 作直线
作直线 ,使得直线
,使得直线 与椭圆
与椭圆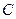 只有一个交点,且
只有一个交点,且 截椭圆
截椭圆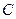 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为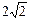 .求出
.求出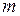 的值.
的值.
.(本小题满分14分)
直棱柱 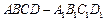 中,底面 ABCD是直角梯形,∠ BAD=∠ ADC=90°,
中,底面 ABCD是直角梯形,∠ BAD=∠ ADC=90°, 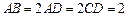 .
.
(Ⅰ)求证: AC⊥平面 BB 1  C 1 C;
C 1 C;
(Ⅱ)若P为 A 1 B 1的中点,求证: DP∥平面 BCB 1,且 DP∥平面 ACB 1.