.(本小题满分14分)
直棱柱 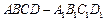 中,底面 ABCD是直角梯形,∠ BAD=∠ ADC=90°,
中,底面 ABCD是直角梯形,∠ BAD=∠ ADC=90°, 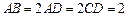 .
.
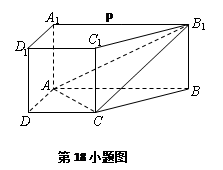
(Ⅰ) 求证: AC⊥平面 BB 1  C 1 C;
C 1 C;
(Ⅱ)若P为 A 1 B 1的中点,求证: DP∥平面 BCB 1,且 DP∥平面 ACB 1.
选修4-1几何证明选讲,如图,D,E分别是AB,AC边上的点,且不与顶点重合,已知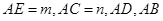 为方程
为方程 的两根,
的两根,
(1)证明 C,B,D,E四点共圆;
(2)若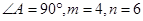 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。
已知抛物线C:y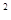 =4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
=4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
(1)求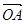 ·
· 的值;(2)设
的值;(2)设 =
=
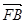 ,求△ABO的面积S的最小值;
,求△ABO的面积S的最小值;
(3)在(2)的条件下若S≤ ,求
,求 的取值范围。
的取值范围。
已知函数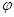 (x)=
(x)=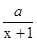 ,a是正常数。(1)若f(x)=
,a是正常数。(1)若f(x)= 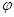 (x)+lnx,且a=
(x)+lnx,且a=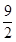 ,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+
,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+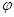 (x),且对任意的x
(x),且对任意的x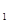 ,x
,x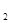 ∈(0,2〕,且x
∈(0,2〕,且x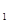 ≠x
≠x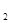 ,都有
,都有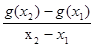 <-1,求a的取值范围
<-1,求a的取值范围
在某次测验中,有6位同学的平均成绩为75分.用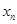 表示编号为
表示编号为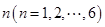 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
成绩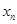 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学成绩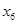 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差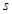 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间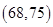 中的概率.
中的概率.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。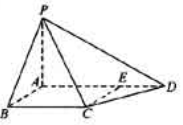
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积