正方体ABCD-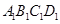 中,求直线
中,求直线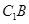 与平面
与平面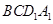 所成的角。
所成的角。
在数列 中,
中,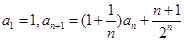
(I)设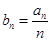 ,求数列
,求数列 的通项公式
的通项公式
(II)求数列 的前
的前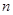 项和
项和
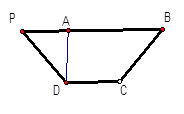
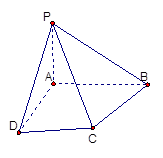
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=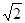 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分 .
.
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5. 同时投掷这两枚玩具一次,记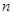 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(Ⅰ)求事件“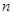 不大于6”的概率;
不大于6”的概率;
(Ⅱ)“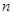 为奇数”的概率和“
为奇数”的概率和“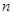 为偶数”的概率是不是相等?证明你的结论.
为偶数”的概率是不是相等?证明你的结论.
设函数 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求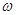 的值.
的值.
(Ⅱ)若函数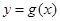 的图像是由
的图像是由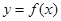 的图像向右平移
的图像向右平移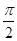 个单位长度得到,求
个单位长度得到,求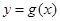 的单调增区间.
的单调增区间.
已知函数f(x)= ;
;
(1)求y=f(x)在点P(0,1)处的切线方程;
(2)设g(x)=f(x)+x-1仅有一个零点,求实数m的值;
(3)试探究函数f(x)是否存在单调递减区间?若有,设其单调区间为[t,s],试求s-t的取值范围?若没有,请说明理由。