某种产品有3只次品和6只正品,每次取出一只测试,直到3只次品全部测出为止,求最后一只次品在第6次测试时被发现的不同的测试情况有多少种.
(本小题14分)
设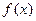 是定义在
是定义在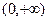 上的单调增函数,满足
上的单调增函数,满足 ,
,
(1)求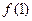 ;
;
(2)若 ,求
,求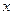 的取值范围。
的取值范围。
(本小题満分15分)
已知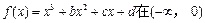 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程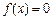 有三
有三 个根,它们分别为
个根,它们分别为 .
.
(1)求c的值;
(2)求证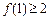 ;
;
(3)求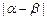 的取值范围
的取值范围
本小题満分15分)
已知 为直角梯形,
为直角梯形,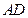 //
// ,
, ,
, 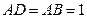 ,
,  ,
,  平面
平面 ,
,
(1)若异面直线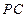 与
与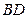 所成的角为
所成的角为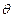 ,且
,且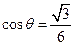 ,求
,求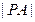 ;
;
(2)在(1)的条件下,设 为
为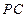 的中点,能否在
的中点,能否在 上找到一点
上找到一点 ,使
,使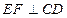 ?
?
(3)在(2)的条件下,求二面角 的大小.
的大小.
 (本小题満分14分)
(本小题満分14分)
二次函数f(x+1)-f(x)=2x,且f(0)=1
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y= f(x)的图像恒在y=2x+m的图像上方,试确定实数m的取值范围。
(本小题満分14分)
已知函数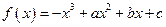 图像上的点
图像上的点 处的切线方程为
处的切线方程为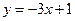 .
.
(1)若函数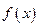 在
在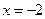 时有极值,求
时有极值,求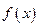 的表达式
的表达式
(2)若函数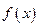 在区间
在区间 上单调递增,求实数
上单调递增,求实数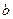 的取值范围
的取值范围