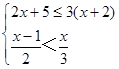如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)试说明△ACB∽△DCE;
(2)请判断EF与AB的位置关系并说明理由.
已知两个连体的正方形(有两条边在同一条直线上)在正方形网格上的位置如图所示,请你把它分割后,拼接成一个新的正方形. (要求:在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上,不写作法).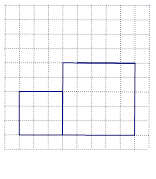
如图,点A、B、C分别是⊙O上的点,∠B=60°, CD是⊙O的直径,P是CD延长线上的点,且AP=AC.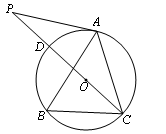
(1)求证:AP是⊙O的切线;
(2)若AC= 3,求PD的长
图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.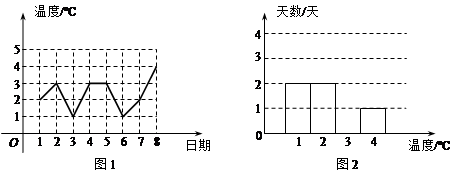
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 ºC;
(3)计算这8天的日最高气温的平均数.
某展览大厅有3个入口和2个出口,其示意图如下. 参观者从任意一个入口进入,参观结束后从任意一个出口离开.
(1)用树状图表示,小明从进入到离开,对于入口和出口的选择有多少种不同的结果?
(2)小明从入口1进入并从出口A离开的概率是多少?
解方程(1)x2+6=5x
(2)9(x-1)2-(x+2)2="0"
(3) +1=
+1= ;
;
(4)解不等式组: