某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值)
(
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 =2,
=2,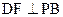 ,垂足为F。
,垂足为F。
(1)求证:PA∥平面BDE。
(2)求证:PB⊥平面DEF。
(3)求二面角B—DE—F的余弦值。
(
在区间[0,1]上给定曲线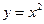 ,
, 轴.
轴.
(1)当面积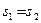 时,求P点的坐标。
时,求P点的坐标。
(2)试在此区间确定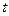 的值,使
的值,使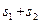 的值最小,并求出最小值。
的值最小,并求出最小值。
已知向量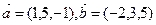 .
.
(1)若
(2)若
(1)当实数 取何值时,复数
取何值时,复数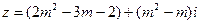 在复平面内对应的点
在复平面内对应的点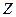 在直线
在直线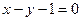 上?
上?
(2)已知 ,如果
,如果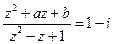 ,求实数
,求实数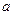 和
和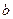 的值。
的值。
(本小题满分14分)
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求f(x)的解析式;
(2)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(3)若当x=1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.