已知四棱锥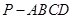 底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,E.F分别是线段AB,BC的中点,
底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,E.F分别是线段AB,BC的中点,
(Ⅰ)证明:PF⊥FD;
(Ⅱ)在PA上找一点G,使得EG∥平面PFD;.
(Ⅲ)若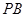 与平面
与平面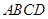 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值.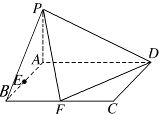
(本小题满分12分)已知函数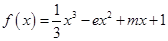 ,
,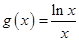 .
.
(Ⅰ)函数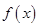 在点
在点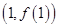 处的切线与直线
处的切线与直线 平行,求函数
平行,求函数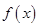 的单调区间;
的单调区间;
(Ⅱ)设函数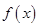 的导函数为
的导函数为 ,对任意的
,对任意的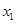 ,
,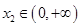 ,若
,若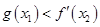 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本题小满分12分)已知椭圆
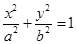 (
(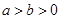 )的一个焦点与抛物线
)的一个焦点与抛物线 的焦点重合,椭圆
的焦点重合,椭圆 上一点到其右焦点
上一点到其右焦点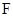 的最短距离为
的最短距离为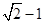 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)记椭圆 的上顶点为
的上顶点为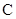 ,是否存在直线
,是否存在直线 交椭圆
交椭圆 于
于 ,
, 两点,使点
两点,使点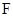 恰好为
恰好为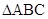 的垂心?若存在,求出直线
的垂心?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)贵阳市某中学高三第一次摸底考试中 名学生数学成绩的频率分布直方图如图
名学生数学成绩的频率分布直方图如图 所示,其中成绩分组区间是
所示,其中成绩分组区间是 ,
, ,
, ,
, ,
, .
.
(Ⅰ)求图中 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这 名学生数学成绩的平均分;
名学生数学成绩的平均分;
(Ⅲ)若这 名学生数学成绩某些分数段的人数(
名学生数学成绩某些分数段的人数( )与语文成绩相应分数段的人数(
)与语文成绩相应分数段的人数( )之比如下表所示,求语文成绩在
)之比如下表所示,求语文成绩在 之外的人数.
之外的人数.

(本小题满分12分)如图所示,四棱锥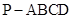 中,底面
中,底面 为平行四边形,
为平行四边形,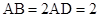 ,
, ,
, 平面
平面 .
.
(Ⅰ)证明:平面 平面
平面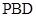 ;
;
(Ⅱ)在 中,
中,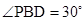 ,点
,点 在
在 上且
上且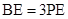 ,求三棱锥
,求三棱锥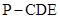 的体积.
的体积.
(本小题满分12分)已知函数 (
( )在
)在 时有最小值
时有最小值 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 所对的边,已知
所对的边,已知 ,
, ,
, ,求角
,求角 的值.
的值.