在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变,纵坐标扩大到原来的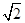 倍后得到点Q(x,
倍后得到点Q(x,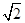 y),且满足
y),且满足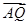 ·
·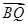 =1.
=1.
(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)过点B作斜率为-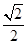 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且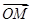 +
+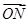 +
+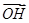 =
=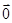 ,试求△MNH的面积.
,试求△MNH的面积.
设数列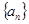 的前
的前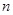 项和
项和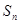 满足:
满足: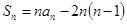 ,等比数列
,等比数列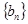 的前
的前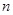 项和为
项和为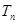 ,公比为
,公比为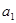 ,且
,且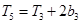 .
.
(1)求数列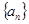 的通项公式;
的通项公式;
(2)设数列 的前
的前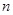 项和为
项和为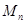 ,求证:
,求证: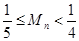 .
.
选修4—5:不等式选讲
设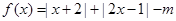 .
.
(1)当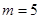 时,解不等式
时,解不等式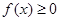 ;
;
(2)若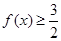 对任意
对任意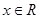 恒成立,求实数
恒成立,求实数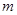 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程
已知曲线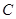 的极坐标方程式
的极坐标方程式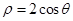 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线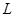 的参数方程是
的参数方程是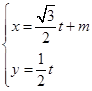 ,(
,( 为参数).
为参数).
(1)求曲线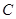 的直角坐标方程和直线
的直角坐标方程和直线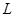 的普通方程;
的普通方程;
(2)设点 ,若直线
,若直线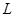 与曲线
与曲线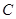 交于两点
交于两点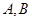 ,且
,且 ,求实数
,求实数 的值.
的值.
已知函数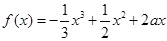 ,其中
,其中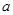 为实常数.
为实常数.
(1)若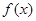 在
在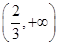 上存在单调递增区间,求
上存在单调递增区间,求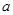 的取值范围;
的取值范围;
(2)当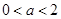 时,若
时,若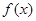 在区间
在区间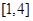 上的最小值为
上的最小值为 ,求
,求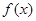 在该区间上的最大值.
在该区间上的最大值.
如下图所示,点 ,
, ,动点
,动点 到点
到点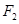 的距离是4,线段
的距离是4,线段 的中垂线交
的中垂线交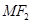 于点
于点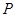 .
.
(1)当点 变化时,求动点
变化时,求动点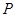 的轨迹
的轨迹 的方程;
的方程;
(2)若斜率为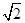 的动直线
的动直线 与轨迹
与轨迹 相交于
相交于 、
、 两点,
两点,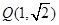 为定点,求
为定点,求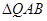 面积的最大值.
面积的最大值.