某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.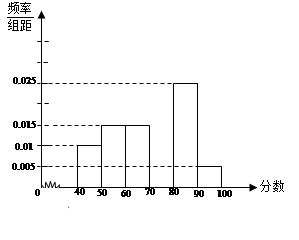
已知函数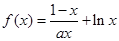 .
.
①若函数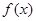 在
在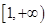 上是增函数,求正实数
上是增函数,求正实数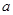 的取值范围;
的取值范围;
②若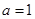 ,
,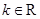 且
且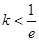 ,设
,设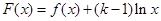 ,求函数
,求函数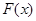 在
在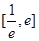 上的最大值和最小值。
上的最大值和最小值。
曲线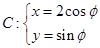 (
(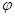 为参数),若点
为参数),若点 是曲线
是曲线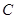 上的动点
上的动点
①求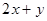 的取值范围
的取值范围
②求直线 被曲线C截得的弦长
被曲线C截得的弦长
某商场销售某种商品的经验表明,该商品每日的销售量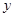 (单位:千克)与销售价格
(单位:千克)与销售价格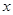 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
①求 的值;
的值;
②若该商品的成本为3元/千克, 试确定销售价格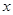 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
已知复数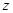 满足:
满足: 求
求 的值
的值
已知曲线 的极坐标方程为
的极坐标方程为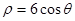 ,曲线
,曲线 的极坐标方程为
的极坐标方程为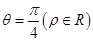 ,曲线
,曲线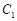 ,
,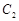 相交于
相交于 ,
, 两点.
两点.
①把曲线 ,
, 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
②求弦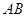 的长度.
的长度.