已知圆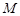 的方程为
的方程为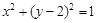 ,直线
,直线 的方程为
的方程为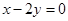 ,点
,点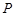 在直线
在直线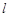 上,过
上,过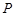 点作圆
点作圆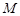 的切线
的切线 ,切点为
,切点为 .
.
(1)若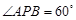 ,试求点
,试求点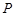 的坐标;
的坐标;
(2)求证:经过 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;
(3)求弦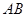 长的最小值.
长的最小值.
在数列 中,
中,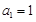 ,且对任意的
,且对任意的 ,
,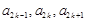 成等比数列,其公比为
成等比数列,其公比为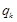 .
.
(1)若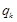 =2(
=2( ),求
),求 ;
;
(2)若对任意的 ,
,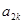 ,
,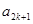 ,
,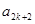 成等差数列,其公差为
成等差数列,其公差为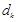 ,设
,设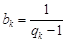 .
.
①求证: 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若 =2,试求数列
=2,试求数列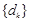 的前
的前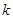 项的和
项的和 .
.
已知函数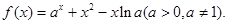
(1)求函数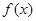 在点
在点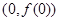 处的切线方程;
处的切线方程;
(2)求函数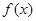 单调递增区间;
单调递增区间;
(3)若存在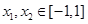 ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数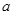 的取值范围.
的取值范围.
已知向量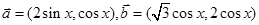 .
.
(1)若 ,且
,且 ,求
,求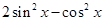 的值;
的值;
(2)定义函数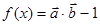 ,求函数
,求函数 的单调递减区间;并求当
的单调递减区间;并求当 时,函数
时,函数 的值域.
的值域.
如图,在正三棱柱ABC-A1B1C1中,A1A=AC,D,E,F分别为线段AC,A1A,C1B的中点.
(1)证明:EF∥平面ABC;
(2)证明:C1E⊥平面BDE.
已知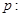 实数
实数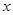 满足
满足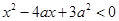 , 其中
, 其中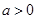 ;
;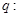 实数
实数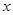 满足
满足 .
.
(1)若 且
且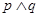 为真, 求实数
为真, 求实数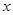 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件, 求实数
的必要不充分条件, 求实数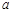 的取值范围.
的取值范围.