如图1,在正方形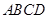 中,对角线
中,对角线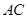 与
与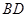 相交于点
相交于点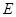 ,
,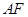 平分
平分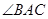 ,交
,交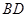 于点
于点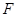 .
.求证:
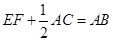 ;
;点
 从点
从点 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点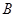 重合),同时点
重合),同时点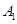 从点
从点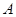 出发,沿着
出发,沿着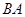 的延长线运动,点
的延长线运动,点 与
与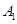 的运动速度相同,当动点
的运动速度相同,当动点 停止运动时,另一动点
停止运动时,另一动点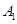 也随之停止运动.如图2,
也随之停止运动.如图2,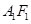 平分
平分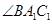 ,交
,交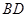 于点
于点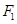 ,过点
,过点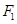 作
作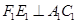 ,垂足为
,垂足为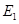 ,请猜想
,请猜想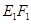 ,
,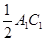 与
与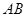 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;在(2)的条件下,当
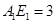 ,
,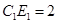 时,求
时,求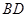 的长.
的长.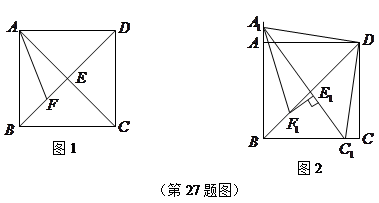
在平面直角坐标系中,∆ABC的顶点坐标是A(-7,1)、B(1,1)、C(1,7),线段DE的端点坐标是D(7,-1)、E(-1,-7)
(1)试说明如何平移线段AC,使其与线段ED重合将线段AC先向______(上,下)平移_______个单位,再向_______(左,右)平移 _______个单位;
(2)将∆ABC绕坐标原点逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的∆DEF,并和∆ABC 同时绕坐标原点O逆时针旋转90o,画出旋转后的图形.
如图,直线y= 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点 是劣弧AO上一动点(
是劣弧AO上一动点( 点与
点与 不重合).抛物线y=-
不重合).抛物线y=- 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,
(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连 交
交 于点
于点 ,延长
,延长 至
至 ,使
,使 ,试探究当点
,试探究当点 运动到何处时,直线
运动到何处时,直线 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.
如图,直线y=-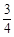 x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4, )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
如图,港口B在港口A的西北方向,上午8时,一艘轮船从港口A出发,以15海里∕时的速度向正北方向航行,同时一艘快艇从港口B出发也向正北方向航行,上午10时轮船到达D处,同时快艇到达C处,测得C处在D处得北偏西30°的方向上,且C、D两地相距100海里,求快艇每小时航行多少海里?(结果精确到0.1海里∕时,参考数据 ≈1.41,
≈1.41,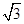 ≈1.73)
≈1.73)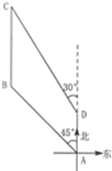
如图,在矩形ABCD中,点E是CD的中点,点F是边AD上一点,连结FE并廷长交BC的延长线于点G,连接BF、BE。且BE⊥FG;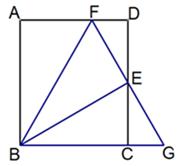
(1)求证:BF=BG。
(2)若tan∠BFG=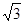 ,S△CGE=6
,S△CGE=6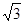 ,求AD的长。
,求AD的长。