如图，直线y＝－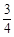
x＋6分别与x轴、y轴交于A、B两点；直线y＝
x与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位的速度沿
轴向左运动．过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN，设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）．
（1）求点C的坐标；
（2）当0＜t＜5时，求S与t之间的函数关系式，并求S的最大值；
（3）当t＞0时，直接写出点（4，
）在正方形PQMN内部时t的取值范围．
图甲是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块全等的小长方形，然后按图乙的形状拼成一个正方形．
（1）图乙的阴影部分的正方形的边长是 ；
（2）用两种不同的方法求阴影部分的面积。
方法一：S阴影=
方法二：S阴影=
（3）观察图乙，请写出代数式（a+b）2、（a-b）2、ab之间的等量关系；
（4）根据（3）题中的等量关系，解决问题：若x+y=10，xy=16，求x-y的值．
如图，△ABC与△DCB中，AC与BD交于点E，且∠A＝∠D，AB＝DC．
（1）求证：△ABE≌DCE；
（2）当∠AEB＝55°时，求∠EBC的度数．
如图，AB＝AC，AD⊥BC于点D，AD＝AE，AB平分∠DAE交DE于点F．请 你写出图中3对全等三角形，并选取其中1对加以证明．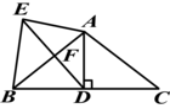
已知a+b=2，ab=-3，求代数式ab3+2a2b2+a3b的值．
已知：如图，在△BAC中，AB=AC，D、E分别是AB、AC的中点，且CD=BE．
求证：∠ADC=∠AEB