已知定点A(-1,0),F(2,0),定直线l:x=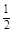 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由.
设函数
(1)若a>0,求函数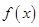 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,求f (x)>b恒成立的概率。
已知函数 .
.
(Ⅰ)设 ,写出数列
,写出数列 的前5项;
的前5项;
(Ⅱ)解不等式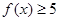 .
.
命题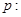 方程
方程 有两个不等的正实数根,命题
有两个不等的正实数根,命题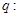 方程
方程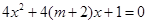 无实数根。若“
无实数根。若“ 或
或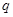 ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率.
(Ⅰ)取到的2只都是次品;
(Ⅱ)取到的2只中恰有一只次品.
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中 120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.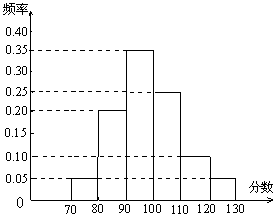
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.