已知反比例函数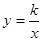
图象过第二象限内的点A（-2，m）AB⊥x轴于B，Rt△AOB面积为3, 若直线y=ax+b经过点A，并且经过反比例函数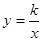的图象上另一点C（n，—
），
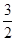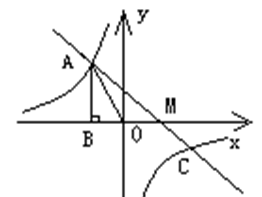
（1）求反比例函数的解析式以及直线y=ax+b的解析式；
（2）求反比例函数的值大于一次函数的值时所对应的x的取值范围。
（3） 自己连接AC、和BC 并求△ABC的面积
解方程：
．
解不等式组
如图，已知在四边形ABCD中，∠B=∠D=90°，AE、CF分别是∠DAB及∠DCB的平分线．则AE与FC有什么关系？请说明理由。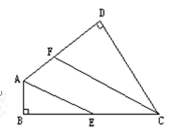
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为面积法．
（1）如图，在等腰三角形ABC中，AB=AC，AC边上的高为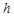
，M是底边BC上的任意一点，点M到腰AB、AC的距离分别为
、
．连接AM,可得结论
+
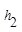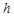=．当点M在BC延长线上时，
、
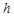、之间的等量关系式是．（直接写出结论不必证明）．
（2）应用：平面直角坐标系中有两条直线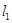
：
、
：
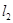，若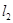上的一点M到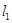的距离是1．请运用（1）的条件和结论求出点M的坐标．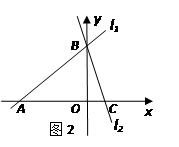
在△ABC中，AB=CB，∠ABC=90º，F为AB延长线上一点，点E在BC上，且AE=CF.
（1）求证：Rt△ABE≌Rt△CBF；
（2）若∠CAE=30º，求∠ACF度数.