五一假期将至,电器市场将火爆.根据市场调查,某商店需进某种电视机和洗衣机,决定电视机的进货量不少于洗衣机进货量的一半,电视机与洗衣机的进价、售价如下表:
| |
电视机 |
洗衣机 |
| 进价(元/台) |
3200 |
2400 |
| 售价(元/台) |
3800 |
2900 |
现计划进电视机和洗衣机共100台,商店最多可凑资金270000元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价外费用)
(2)哪种进货方案待商店销售完进的电视机与洗衣机后获得利润最大?并求出最大利润.
某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
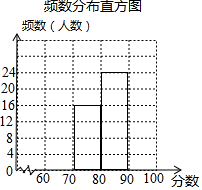
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
|
分数段 |
频数(人数) |
|
|
|
|
|
16 |
|
|
24 |
|
|
|
请解答下列问题:
(1)完成频数分布表, , .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩 范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
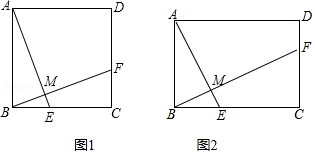
(1)如图1,在正方形 中,点 , 分别在 , 上, 于点 ,求证: ;
(2)如图2,将 (1)中的正方形 改为矩形 , , , 于点 ,探究 与 的数量关系,并证明你的结论.
直线 的解析式为 ,分别交 轴、 轴于点 , .
(1)写出 , 两点的坐标,并画出直线 的图象;
(2)将直线 向上平移4个单位得到 , 交 轴于点 .作出 的图象, 的解析式是 .
(3)将直线 绕点 顺时针旋转 得到 , 交 于点 .作出 的图象, .

已知抛物线 与 轴交于点 和点 .
(1)求抛物线 的函数解析式;
(2)如图①,将抛物线 沿 轴翻折得到抛物线 ,抛物线 与 轴交于点 ,点 是线段 上的一个动点,过点 作 轴交抛物线 于点 ,求线段 的长度的最大值;
(3)在(2)的条件下,当线段 处于长度最大值位置时,作线段 的垂直平分线交 于点 ,垂足为 ,点 是抛物线 上一动点, 与直线 相切,且 ,求满足条件的所有点 的坐标.
