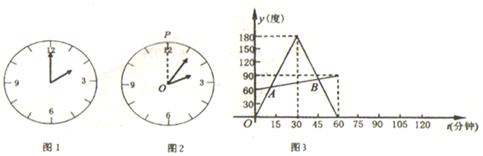
小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1度,时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式:
请你完成:求出图3中y2与t的函数关系式;
直接写出A、B两点的坐标,并解释这两点的实际意义;
若小华继续观察一个小时,请你在题图3中补全图象.
如图,已知正方形ABCD的边长为5,且∠EAF=45 ,把△ABE绕点A逆时针旋转90
,把△ABE绕点A逆时针旋转90 ,落在
,落在 ADG的位置.
ADG的位置.
(1)请在图中画出 ADG.
ADG.
(2)证明:∠GAF=45 .
.
(3)求点A到EF的距离AH.
如图,利用一面长 的墙,用
的墙,用 长的篱笆,围成一个长方形的养鸡场.
长的篱笆,围成一个长方形的养鸡场.
(1)怎样围成一个面积为 的长方形养鸡场?
的长方形养鸡场?
(2)能否围成一个面积为 的长方形养鸡场?如能,说明围法;如不能,请说明理由.
的长方形养鸡场?如能,说明围法;如不能,请说明理由.
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转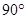 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
已知关于x的一元二次方程x2 = 2(1-m)x-m2 的两实数根为x1,x2.
(1)求m的取值范围;
(2)设y = x1 + x2,当y取得最小值时,求相应m的值,并求出最小值.
已知关于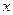 的一元二次方程
的一元二次方程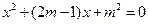 有两个实数根
有两个实数根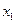 和
和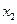 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当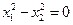 时,求
时,求 的值
的值