如图,在正方体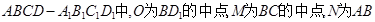 的中点,P为BB1的中点.
的中点,P为BB1的中点.
(I)求证: ;
;
(II)求证 ;
;
(本小题满分12分)已知椭圆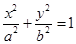 (
( )的离心率
)的离心率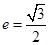 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点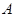
 的直线
的直线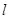 与椭圆相交另一点
与椭圆相交另一点 ,若
,若 ,求直线
,求直线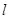 的倾斜角.
的倾斜角.
((本小题满分12分)当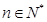 时,
时,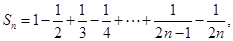
 .
.
(I)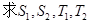 ;(II)
;(II) .
.
(本小题满分12分)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(I)证明:平面PQC⊥平面DCQ;
(II)求平面QBP与平面BPC夹角的余弦值.
((本题14分)如图4,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为 ;
;
(Ⅲ)是否存在常数 ,使得
,使得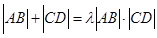 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
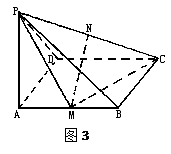
((本题14分)如图3,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=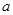 。
。
(Ⅰ)求证:MN//平面PAD;
(Ⅱ)求证:平面PMC⊥平面PCD;
(Ⅲ)若二面角P—MC—A是60°的二面角,求四棱锥P—ABCD的体积。