设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.
已知椭圆C: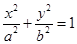 的离心率等于
的离心率等于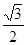 ,点P
,点P 在椭圆上。
在椭圆上。
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左右顶点分别为
的左右顶点分别为 ,过点
,过点 的动直线
的动直线 与椭圆
与椭圆 相交于
相交于 两点,是否存在定直线
两点,是否存在定直线 :
: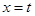 ,使得
,使得 与
与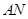 的交点
的交点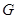 总在直线
总在直线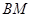 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的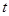 值;若不存在,说明理由.
值;若不存在,说明理由.
如图已知:菱形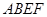 所在平面与直角梯形
所在平面与直角梯形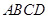 所在平面互相垂直,
所在平面互相垂直,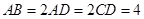 ,
, 点
点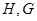 分别是线段
分别是线段 的中点.
的中点. 
(1)求证:平面
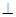 平面
平面 ;
;
(2)点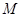 在直线
在直线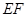 上,且
上,且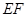 //平面
//平面 ,求平面
,求平面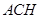 与平面
与平面 所成角的余弦值。
所成角的余弦值。
右表是一个由正数组成的数表,数表中各行依次成等差数列,各列依次成等比数列,且公比都相等,已知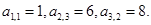
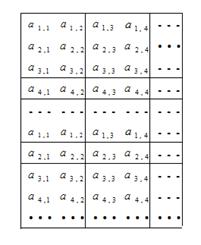
(1)求数列 的通项公式;
的通项公式;
(2)设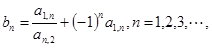 求数列
求数列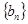 的前
的前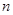 项和
项和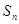 。
。
已知向量
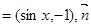
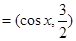 ,
,
(1)当 时,求函数
时,求函数 的值域:
的值域:
(2)锐角 中,
中, 分别为角
分别为角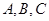 的对边,若
的对边,若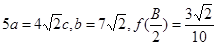 ,求边
,求边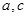 .
.
南昌市为增强市民的交通安全意识,面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通,把符合条件的1000名志愿者按年龄分组:第1组 、第2组
、第2组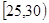 、第3组
、第3组 、第4组
、第4组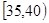 、第5组
、第5组 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,南昌市决定在这12名志愿者中随机抽取3名志愿者到学校宣讲交通安全知识,若 表示抽出的3名志愿者中第3组的人数,求
表示抽出的3名志愿者中第3组的人数,求 的分布列和数学期望.
的分布列和数学期望.