为了测量学校一棵参天古树的高度，我校数学兴趣小组做了如下探索：
实践1：利用一根标竿和一根皮尺设计出如图1的测量方案，把长为2.5米的标竿竖直插入离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时眼睛恰好通过标竿顶点F，看到树的顶点A。再用皮尺测得DE＝2.7米。观察者目高CD＝1.6米。他们利用相似原理求得树高为5.4米。
实践2：提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案，并根据你所设计的测量方案回答下列问题。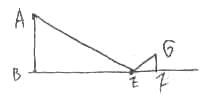
（1）在你设计的方案中，选用的测量工具是（用工具的序号填写） 。
（2）在图2中画出你测量方案的示意图。
（3）你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据 。
（4）写出求树高（AB）的等式，AB＝ 。（用a、b、c等字母表示）
在一副扑克牌中，拿出红桃2、红桃3、红桃4、红桃5四张牌，小明从中随机摸出一张记下牌面上的数字为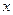
，然后放回洗匀，再由小华随机摸出一张，记下牌面上的数字为
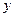，组成一对数（，）。
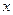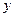（1）用列表法或树状图表示出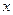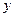（，）的所有可能出现的结果；
（2）求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率。
如图，点D在双曲线上，AD垂直
轴，垂足为
A，点C在AD上，CB平行于轴交双曲线于点B，直线AB与
轴交于点F，已知AC：
AD=1：3，点C的坐标为（2，2）。
（1）求该双曲线的解析式；
（2）求△OFA的面积。
益趣玩具店购进一种儿童玩具，计划每个售价
36元，能盈利80﹪，在销售中出现了滞销，于是先后两次降价，售价降为25元。
（1）求这种玩具的进价。
（2）求平均每次降价的百分率（精确到0.1﹪）
如图，一架满载救援物资的飞机到达灾区的上空，在
A处测得空投地点C的俯角
=60°，测得地面指挥台B的俯角
=30°。已知BC的距离是2000米，求此时飞机的高度（结果保留根号）
（1）计算：
