已知集合 ,集合
,集合 .
.
(1) 求当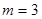 时,
时,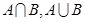 ; (2) 若
; (2) 若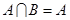 ,求实数
,求实数 的取值范围.
的取值范围.
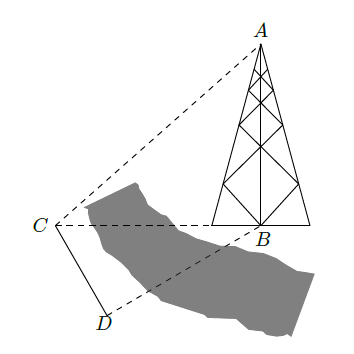
如图,测量河对岸的塔高
时,可以选与塔底
在同一水平面内的两个测点
与
. 现测得
,
,
,并在点
测得塔顶
的仰角为
,求塔高
. 
已知函数
,
、
是方程
的两个根(
),
是
的导数,设
,
(n=1,2,…),
(Ⅰ)求 、 的值;
(Ⅱ)已知对任意的正整数 有 ,记 ,求数列 的前 项和 .
已知 是实数,函数 ,如果函数 在区间 上有零点,求实数 的取值范围。
如图所示,等腰三角形
的底边
,高
.点
是线段
上异于
的动点.点
在
边上,且
.现沿
将
折起到
的位置,使
.
记
表示四棱锥
的体积。
(1)求
的表达式;
(2)当
为何值时,
取得最大值?
(3)当
取得最大值时,求异面直线
与
所成角的余弦值。 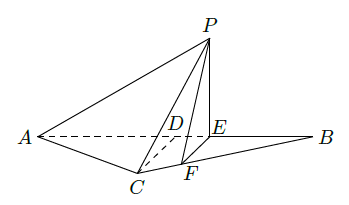
在直角坐标系
中,已知圆心在第二象限、半径为
的圆
与直线
相切于坐标原点
.椭圆
与圆
的一个交点到椭圆两焦点的距离之和为10.
(1)求圆
的方程;
(2)试探究圆
上是否存在异于原点的点
,使
到椭圆的右焦点
的距离等于线段
的长,若存在求出
的坐标;若不存在,请说明理由.