已知函数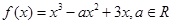 .
.
(Ⅰ)若函数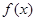 是R上的单调递增函数,求实数的
是R上的单调递增函数,求实数的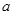 的取值范围;
的取值范围;
(Ⅱ)若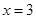 是
是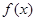 的一个极值点,求
的一个极值点,求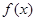 在
在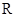 上的极大值与极小值
上的极大值与极小值
(本小题满分10分)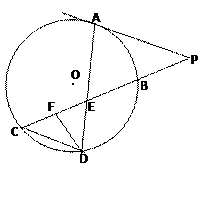
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE·EB=EF·EP.
(本小题满分12分)
已知函数
(Ⅰ)若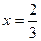 为
为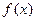 的极值点,求实数
的极值点,求实数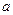 的值;
的值;
(Ⅱ)若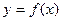 在
在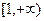 上为增函数,求实数
上为增函数,求实数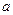 的取值范围;
的取值范围;
(Ⅲ)若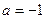 使,方程
使,方程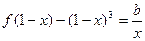 有实根,求实数
有实根,求实数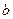 的取值范围.
的取值范围.
(本小题12分)
已知椭圆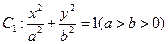 的长轴长为
的长轴长为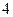 ,离心率为
,离心率为 ,
,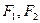 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点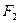 ,且与直线
,且与直线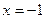 相切.
相切.
(Ⅰ)(ⅰ)求椭圆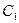 的方程; (ⅱ)求动圆圆心轨迹
的方程; (ⅱ)求动圆圆心轨迹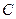 的方程;
的方程;
(Ⅱ) 在曲线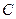 上有两点M、N,椭圆C上有两点P、Q,满足
上有两点M、N,椭圆C上有两点P、Q,满足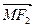 与
与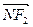 共线,
共线,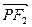 与
与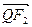 共线,且
共线,且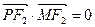 ,求四边形
,求四边形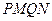 面积的最小值.
面积的最小值.
(本小题12分)
如图,已知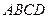 为平行四边形,
为平行四边形,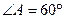 ,
,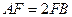 ,
,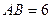 ,点
,点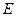 在
在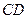 上,
上,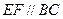 ,
, ,
,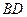 与
与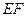 相交于
相交于 .现将四边形
.现将四边形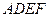 沿
沿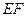 折起,使点
折起,使点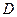 在平面
在平面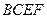 上的射影恰在直线
上的射影恰在直线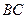 上.
上.
(Ⅰ)求证: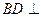 平面
平面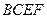 ;
;
(Ⅱ)求折后直线DN与直线BF所成角的余弦值;
(Ⅲ)求三棱锥N—ABF的体积.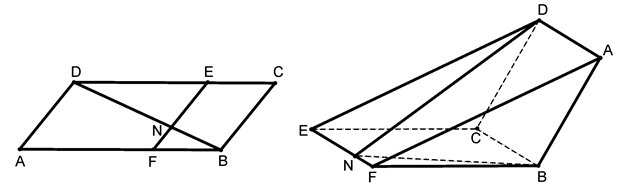
(本小题12分)
盒子中装着标有数字1、2、3、4的卡片分别有1张、2张、3张、4张,从盒子中任取3张卡片,每张卡片被取出的可能性都相等,用 表示取出的3张卡片的最大数字,求:
表示取出的3张卡片的最大数字,求:
(Ⅰ)取出的3张卡片上的数字互不相同的概率;
(Ⅱ)随机变量 的概率分布和数学期望;
的概率分布和数学期望;
(Ⅲ)设取出的三张卡片上的数字之和为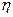 ,求
,求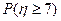 .
.