（本小题12分）
盒子中装着标有数字1、2、3、4的卡片分别有1张、2张、3张、4张，从盒子中任取3张卡片，每张卡片被取出的可能性都相等，用
表示取出的3张卡片的最大数字，求：
（Ⅰ）取出的3张卡片上的数字互不相同的概率；
（Ⅱ）随机变量的概率分布和数学期望；
（Ⅲ）设取出的三张卡片上的数字之和为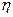
，求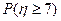
．
已知A、B、C是直线l上的三点，且|AB|=|BC|=6，⊙O′切直线l于点A，又过B、C作⊙O′异于l的两切线，设这两切线交于点P，求点P的轨迹方程.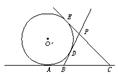
已知P(4，0)是圆x2+y2=36内的一点，A、B是圆上两动点，且满足∠APB=90°，求矩形APBQ的顶点Q的轨迹方程.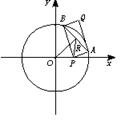
如图，已知ABCD是矩形，AB=a,AD=b,PA⊥平面ABCD，PA=2c,Q是PA的中点.
求：(1)Q到BD的距离；
(2)P到平面BQD的距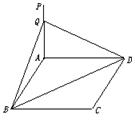
如图，在梯形ABCD中，AD∥BC，∠ABC=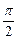
,AB= 
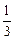AD=a,
∠ADC=arccos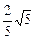
,PA⊥面ABCD且PA=a.
(1)求异面直线AD与PC间的距离；
(2)在线段AD上是否存在一点F，使点A到平面PCF的距离为
如图，已知三棱柱A1B1C1—ABC的底面是边长为2的正三角形，侧棱A1A与AB、AC均成45°角，且A1E⊥B1B于E，A1F⊥CC1于F.
(1)求点A到平面B1BCC1的距离；
(2)当AA1多长时，点A1到平面ABC与平面B1BCC1的距离相等.