已知梯形ABCD中,AD∥B C,AB=AD(如图所示),∠BAD的平分线AE交BC于点E,连接DE.
C,AB=AD(如图所示),∠BAD的平分线AE交BC于点E,连接DE.
(1)在下图中,用尺规作∠BAD的平分线AE(保留作图痕迹不写作法),并证明四边形ABED是菱形.
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.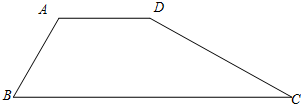
 解不等式组
解不等式组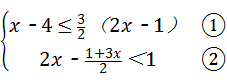 ,把解集表
,把解集表
示在数轴上, 并求出不等式组的整数解.
并求出不等式组的整数解.
先化简,再求值: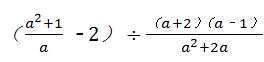 ,其中a2﹣4=0.
,其中a2﹣4=0.
在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是BC上的一个动点(不与B、C重合),过F点的反比例函数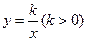 的图象与AC边交于点E.
的图象与AC边交于点E.
(1)求证:AE•AO=BF•BO;
(2)若点E的坐标为(2,4),求经过O、E、F三点的抛物线的解析式;
(3)是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出此时的OF的长:若不存在,请说明理由.
如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD= cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.