选修4-4:坐标系与参数方程
已知直线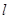 的参数方程为
的参数方程为 (t为参数),若以平面直角坐标系
(t为参数),若以平面直角坐标系 的O点为极点,
的O点为极点, 轴正半轴为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
轴正半轴为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为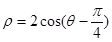 。
。
(1)求直线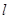 的倾斜角;
的倾斜角;
(2)若直线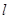 与曲线C交于不同的两点A,B,求AB的长。
与曲线C交于不同的两点A,B,求AB的长。
已知函数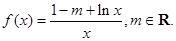
(I)若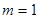 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性;
(II)若函数在 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。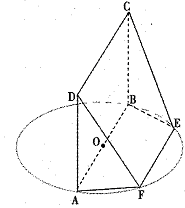
(I)求证:BF⊥平面DAF;
(II)求多面体ABCDFE的体积。
已知函数
(I)若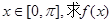 的最大值和最小值;
的最大值和最小值;
(II)若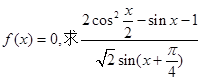 的值。
的值。
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如下表:
| 寿命(h) |
频率 |
| 500600 |
0.10 |
| 600700 |
0.15 |
| 700800 |
0.40 |
| 800900 |
0.20 |
| 9001000 |
0.15 |
| 合计 |
1 |

(I)在下图中补齐频率分布直方图;
(II)估计元件寿命在500800h以内的概率。
在直角坐标系xoy中,直线 的参数方程为
的参数方程为 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为 ,求|PA|+|PB|。
,求|PA|+|PB|。