在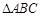 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且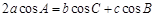 .
.
(1)求角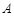 的大小;
的大小;
(2)若 ,求
,求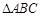 的面积.
的面积.
已知函数 (
( ),其中
),其中 .
.
(1)若曲线 与
与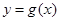 在点
在点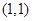 处相交且有相同的切线,求
处相交且有相同的切线,求 的值;
的值;
(2)设 ,若对于任意的
,若对于任意的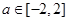 ,函数
,函数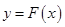 在区间
在区间 上的值恒为负数,求
上的值恒为负数,求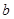 的取值范围.
的取值范围.
如图,已知圆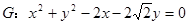 ,经过椭圆
,经过椭圆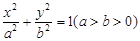 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点 倾斜角为
倾斜角为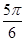 的直线
的直线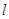 交椭圆于C,D两点,
交椭圆于C,D两点,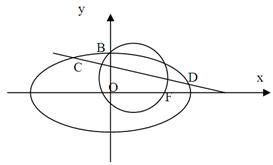
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE= .
.
(1)若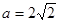 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;
(2)求实数 的值,使得二面角AECD的大小为60°.
的值,使得二面角AECD的大小为60°.
已知等差数列 的公差不为零,其前n项和为
的公差不为零,其前n项和为 ,若
,若 =70,且
=70,且 成等比数列,
成等比数列,
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,求证:
,求证: .
.