某公司为了了解职工的年龄分布,在甲乙两部门各随机抽取10名职工,统计他们的年龄,绘成茎叶图如右图所示:
(Ⅰ)求甲部门职工年龄的众数与乙部门职工年龄的中位数.
(Ⅱ)请判断哪个部门的职工年龄更年轻化,并说明你的理由.
(本小题满分14分).已知函数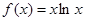 ,
, (a为实数).
(a为实数).
(Ⅰ)当a=5时,求函数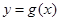 在
在 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间[t,t+2](t >0)上的最小值;
在区间[t,t+2](t >0)上的最小值;
(Ⅲ)若存在两不等实根 ,使方程
,使方程 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(本小题满分13分)已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为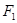 和
和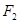 ,且|
,且|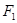
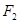 |=2,点(1,
|=2,点(1, )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过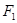 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若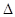 A
A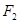 B的面积为
B的面积为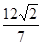 ,求以
,求以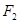 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
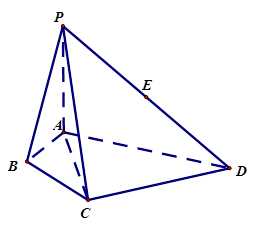
(本小题满分12分)如图,在四棱锥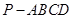 中,
中,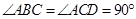 ,
, ,
,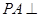 平面
平面 ,
,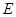 为
为 的中点,
的中点,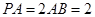 .
.
(1)求证: ∥平面
∥平面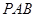 ;
;
(2)求四面体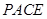 的体积.
的体积.
(本小题满分12分)已知数列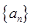 的前
的前 项和
项和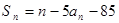 ,
,
(Ⅰ)求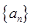 的通项公式;
的通项公式;
(Ⅱ)令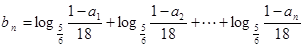 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)已知函数 ,
,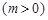 的最大值为2.
的最大值为2.
(Ⅰ)求函数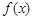 在
在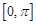 上的值域;
上的值域;
(Ⅱ)已知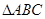 外接圆半径
外接圆半径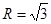 ,
,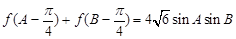 ,角
,角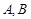 所对的边分别是
所对的边分别是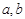 ,求
,求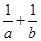 的值.
的值.