如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.画出对称中心E,并写出点E、A、C的坐标
P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2、C2的坐标;
判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).

在□ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
如图,在平面直角坐标系中,顶点为(4,-1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3)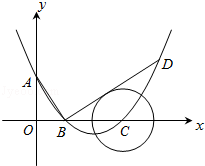
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△DEF是直角三角形时,求x的值.
如图,点A,B,C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1.景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度是指坡面的铅直高度与水平宽度的比.)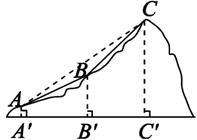
为了提高学生书写汉字的能力,增强保护汉字的意识,某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:

请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.