已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
如图,四棱锥 中,
中, 平面
平面 ,
, 与底面所成的角为
与底面所成的角为 ,底面
,底面 为直角梯形,
为直角梯形, ,
,
(1)求证:平面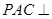 平面
平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使
,使 与平面
与平面 所成的角为
所成的角为 ?若存在,确定点
?若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
已知函数f(x)=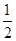 sin2xsinφ+cos2xcosφ-
sin2xsinφ+cos2xcosφ-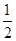 sin
sin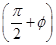 (0<φ<π),其图象过点
(0<φ<π),其图象过点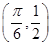 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的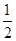 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在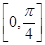 上的最大值和最小值.
上的最大值和最小值.
(1)求不等式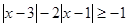 的解集;
的解集;
(2)已知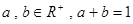 ,求证:
,求证: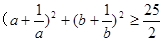 .
.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (t为参数).在极坐标系(与直角坐标系
(t为参数).在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为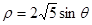
(1)求直线 及圆
及圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线 交于点
交于点 .若点
.若点 的坐标为(3,
的坐标为(3, ),求
),求 .
.
如图,AB是
 的一条切线,切点为B,直线ADE, CFD,CGE都是
的一条切线,切点为B,直线ADE, CFD,CGE都是
 的割线,已知AC=AB.
的割线,已知AC=AB.
(1)求证:FG//AC;
(2)若CG=1,CD=4,求 的值.
的值.