某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：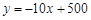
．
（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）
问题探究
（1）请在图①的正方形
内，画出使
的一个点
，并说明理由．
（2）请在图②的正方形内（含边），画出使
的所有的点，并说明理由．
问题解决
（3）如图③，现在一块矩形钢板
．工人师傅想用它裁出两块全等的、面积最大的
和
钢板，且
．请你在图③中画出符合要求的点和
，并求出的面积（结果保留根号）．
如图，在平面直角坐标系中，
，且
，点
的坐标是
．
（1）求点
的坐标；
（2）求过点
的抛物线的表达式；
（3）连接
，在（2）中的抛物线上求出点
，使得
．
如图，
是
的外接圆，
，过点
作
，交
的延长线于点
．
（1）求证：
是的切线；
（2）若的半径
，求线段的长．
甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由．
在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回．设汽车从甲地出发
（h）时，汽车与甲地的距离为
（km），与的函数关系如图所示．
根据图象信息，解答下列问题：
（1）这辆汽车的往、返速度是否相同？请说明理由；
（2）求返程中与之间的函数表达式；
（3）求这辆汽车从甲地出发4h时与甲地的距离．