在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.

⑴求证:Rt△ABE≌Rt△CBF;
⑵若∠CAE=30º,求∠ACF度数.
在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园与墙平行的一边长为x(m),花园的面积为y(m2)。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由:
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大?最大面积是多少?
用配方法解方程: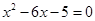 .
.
为了预防流感,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图),现测药物8分钟燃毕,此时空气中每立方米含药量为6毫克,请根据题中所提供的信息,回答下列问题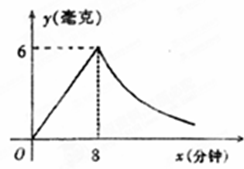
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围是 ;药物燃烧完后,y与x的函数关系式为
(2)研究表明,当空气中的每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室.
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效地杀灭空气中的病菌,那么此次消毒是否有效?为什么?
已知下列n(n为正整数)个关于x的一元二次方程: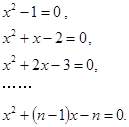
(1)请解上述一元二次方程;
(2)请你指出这n个方程的根具有什么共同特点,写出一条即可
端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量特设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上重转),当两个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.
(1)用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果.
(2)若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少?