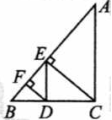
在Rt△ACB和Rt△AEF中，∠ACB∠AEF90°，若点-优题课

在Rt△ACB和Rt△AEF中，∠ACB=∠AEF=90°，若点P是BF的中点，连接PC，PE．
特殊发现：如图1，若点E，F分别落在边AB，AC上，则结论：PC=PE成立（不要求证明）．
问题探究：把图1中的△AEF绕着点A顺时针旋转．
（1）如图2，若点E落在边CA的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由；
（2）如图3，若点F落在边AB上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
（3）记，当k为何值时，△CPE总是等边三角形？（请直接写出k的值，不必说明理由）

科目数学题型解答题难度中等

如图，在平面直角坐标系中已知点 $B (- 2, 4)$ ，四边形 $ABCO$ 是长方形，点 $D$ 从 $O \to C \to B$ 运动，速度为 $1$ （单位 $/ s$ ）.

（1）当 $D$ 在 $OC$ 上运动时，直线 $BD$ 能否将长方形 $ABCD$ 的面积分为 $1 : 2$ 两部分，若能，求 $D$ 点坐标，若不能，说明理由；

（2）点 $D$ 运动到 $CB$ 时，何时 $△ ABD$ 的面积等于 $\frac{1}{4}$ 矩形面积?并求此时 $D$ 点坐标．

设等式 $\sqrt{a (x - a)} + \sqrt{a (y - a)} = \sqrt{x - a} - \sqrt{a - y}$ 在实数范围内成立，其中 $a, x, y$ 是两两不同的实数，求 $\frac{3 x^{2} + xy - y^{2}}{x^{2} - xy + y^{2}}$ 的值．

如图，在 $△ ABC$ 中， $CE ⊥ AB$ 于 $E, DF ⊥ AB$ 于 $F, AC / / ED, CE$ 是 $∠ ACB$ 的角平分线，求证： $∠ EDF = ∠ BDF$ ．

一只青蛙在平面直角坐标系上从点 $(1, 1)$ 开始，可以按照如下两种方式跳跃：①能从任意一点 $(a, b)$ ，跳到点 $(2 a, b)$ 或 $(a, 2 b)$ ；②对于点 $(a, b)$ ，如果 $a > b$ ，则能从 $(a, b)$ 跳到 $(a - b, b)$ ，如果 $a < b$ ，则能从 $(a, b)$ 跳到 $(a, b - a)$ ，例如，按照上述跳跃方式，这只青蛙能够到达点 $(3, 1)$ ，跳跃的一种路径为: $(1, 1) \to (2, 1) \to (4, 1) \to (3, 1)$ ，请你思考：这只青蛙按照规定的两种方式跳跃，能达到下列各点吗?如果能，请分别给出从点 $(1, 1)$ 出发到指定点的路径；如果不能，请说明理由．

（1） $(3, 5)$ ；（2） $(12, 60)$ ；（3） $(200, 5)$ ；（4） $(200, 6)$ ．

如果将点 $P$ 绕定点 $M$ 旋转 $180^{\circ}$ 后与点 $Q$ 重合，那么称点 $P$ 与点 $Q$ 关于点 $M$ 对称，定点 $M$ 叫对称中心，此时，点 $M$ 是线段 $PQ$ 的中点，如图，在直角坐标系中， $△ ABO$ 的顶点 $A, B, O$ 的坐标分别为 $(1, 0), (0, 1), (0, 0)$ ，点列 $P_{1}, P_{2}, P_{3}, \dots$ 中的相邻两点都关于 $△ ABO$ 的一个顶点对称，点 $P_{1}$ 与点 $P_{2}$ 关于点 $A$ 对称，点 $P_{2}$ 与点 $P_{3}$ 关于点 $B$ 对称，点 $P_{3}$ 与点 $P_{4}$ 关于点 $O$ 对称，点 $P_{4}$ 与点 $P_{5}$ 关于点 $A$ 对称，点 $P_{5}$ 与点 $P_{6}$ 关于点 $B$ 对称，点 $P_{6}$ 与点 $P_{7}$ 关于点 $O$ 对称，…，对称中心分别是 $A, B, O, A, B, O, \dots$ ，且这些对称中心依次循环，已知 $P_{1}$ 的坐标为 $(1, 1)$ ，试写出 $P_{2}, P_{7}, P_{100}, P_{2021}$ 的坐标．

试卷网试题网古诗词网作文网范文网